

Research in the lab is based on a computational model of object recognition in cortex (Riesenhuber & Poggio, Nature Neuroscience, 1999), dubbed HMAX ("Hierarchical Model and X") by Mike Tarr (Nature Neuroscience, 1999) in his News & Views on the paper. Since we didn't think of a better name beforehand, HMAX stuck. Oh well...
The model summarizes the basic facts about the ventral visual stream, a hierarchy of brain areas thought to mediate object recognition in cortex. It was originally developed to account for the experimental data of Logothetis et al. (Cerebral Cortex, 1995) on the invariance properties and shape tuning of neurons in macaque inferotemporal cortex, the highest visual area in the ventral stream. In the meantime, the model has been shown to predict several other experimental results and provide interesting perspectives on still other data and claims. The model is used as a basis in a variety of projects in our and other labs.
The goal is to explain cognitive phenomena in terms of simple and well-understood computational processes in a physiologically plausible model. Thus, the model is a tool to integrate and interpret existing data and to make predictions to guide new experiments. Clearly, the road ahead will require a close interaction between model and experiment. Towards this end, this web site provides background information on HMAX, including the source code, and further references:
Our collaborators in Tommy Poggio's group at MIT have done some really nice work with the model, in particular its application to machine vision problems. Please click here for an overview of their software and papers on the topic (look for "Model of Object Recognition").
Object recognition in cortex is thought to be mediated by the ventral visual pathway (Ungerleider, 1994) running from primary visual cortex, V1, over extrastriate visual areas V2 and V4 to inferotemporal cortex, IT. Based on physiological experiments in monkeys, IT has been postulated to play a central role in object recognition. IT in turn is a major source of input to PFC, "the center of cognitive control" (Miller, 2000) involved in linking perception to memory.
Over the last decades, several physiological studies in non-human primates have established a core of basic facts about cortical mechanisms of recognition that seem to be widely accepted and that confirm and refine older data from neuropsychology. A brief summary of this consensus knowledge begins with the groundbreaking work of Hubel and Wiesel first in the cat (Hubel, 1962, 1965) and then in the macaque (Hubel, 1968). Starting from simple cells in primary visual cortex, V1, with small receptive fields that respond preferably to oriented bars, neurons along the ventral stream (Perrett, 1993; Tanaka, 1996; Logothetis, 1996) show an increase in receptive field size as well as in the complexity of their preferred stimuli (Kobatake, 1994). At the top of the ventral stream, in anterior inferotemporal cortex (AIT), cells are tuned to complex stimuli such as faces (Gross, 1972; Desimone, 1984, 1991; Perrett, 1992). A hallmark of these IT cells is the robustness of their firing to stimulus transformations such as scale and position changes (Tanaka, 1996; Logothetis, 1995, 1996; Perrett, 1993). In addition, as other studies have shown (Perrett, 1993; Booth, 1998; Logothetis, 1995; Hietanen 1992), most neurons show specificity for a certain object view or lighting condition.
A comment about the architecture is important: In its basic, initial operation - akin to "immediate recognition" - the hierarchy is likely to be mainly feedforward (though local feedback loops almost certainly have key roles) (Perrett, 1993). ERP data (Thorpe, 1996) have shown that the process of object recognition appears to take remarkably little time, on the order of the latency of the ventral visual stream (Perrett, 1992), adding to earlier psychophysical studies using a rapid serial visual presentation (RSVP) paradigm (Potter, 1975; Intraub, 1981) that have found that subjects were still able to process images when they were presented as rapidly as 8/s.
In summary, the accumulated evidence points to six mostly accepted properties of the ventral stream architecture:
These basic facts lead to a Standard Model, likely to represent the simplest class of models reflecting the known anatomical and biological constraints. It represents in its basic architecture the average belief - often implicit - of many visual physiologists. In this sense it is definitely not "our" model. The broad form of the model is suggested by the basic facts; we have made it quantitative, and thereby predictive (through computer simulations).
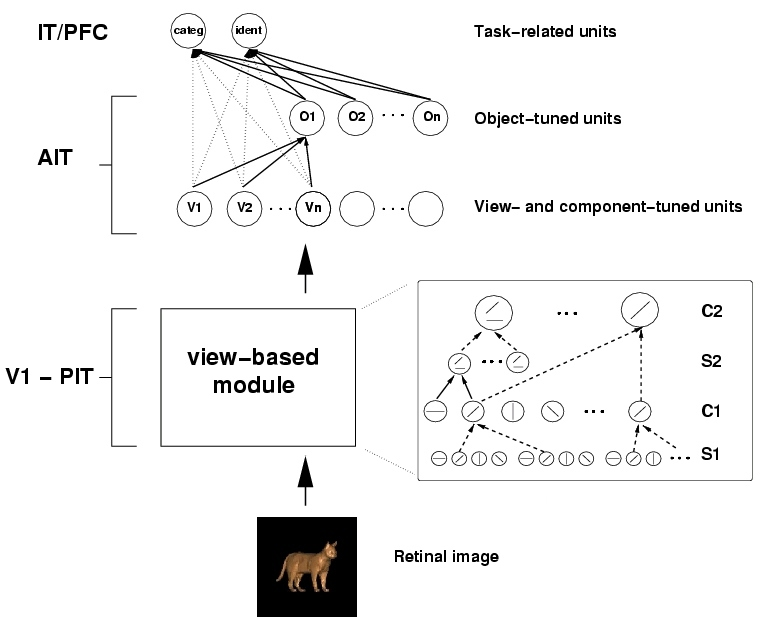
Figure 1: schematic of the Standard Model
The model reflects the general organization of visual cortex in a series of layers from V1 to IT to PFC. From the point of view of invariance properties, it consists of a sequence of two main modules based on two key ideas. The first module, shown schematically above, leads to model units showing the same scale and position invariance properties as the view-tuned IT neurons of (Logothetis, 1995), using the same stimuli. This is not an independent prediction since the model parameters were chosen to fit Logothetis' data. It is, however, not obvious that a hierarchical architecture using plausible neural mechanisms could account for the measured invariance and selectivity. Computationally, this is accomplished by a scheme that can be best explained by taking striate complex cells as an example: invariance to changes in the position of an optimal stimulus (within a range) is obtained in the model by means of a maximum operation (max) performed on the simple cell inputs to the complex cells, where the strongest input determines the cell's output. Simple cell afferents to a complex cell are assumed to have the same preferred orientation with their receptive fields located at different positions. Taking the maximum over the simple cell afferent inputs provides position invariance while preserving feature specificity. The key idea is that the step of filtering followed by a max operation is equivalent to a powerful signal processing technique: select the peak of the correlation between the signal and a given matched filter, where the correlation is either over position or scale. The model alternates layers of units combining simple filters into more complex ones - to increase pattern selectivity with layers based on the max operation - to build invariance to position and scale while preserving pattern selectivity.
In the second part of the architecture, shown above, learning from multiple examples, i.e., different view-tuned neurons, leads to view-invariant units as well as to neural circuits performing specific tasks. The key idea here is that interpolation and generalization can be obtained by simple networks, similar to Gaussian Radial Basis Function networks (Poggio, 1990) that learn from a set of examples, that is, input-output pairs. In this case, inputs are views and the outputs are the parameters of interest such as the label of the object or its pose or expression (for a face). The Gaussian Radial Basis Function (GRBF) network has a hidden unit for each example view, broadly tuned to the features of an example image (see also deBeeck (2001)). The weights from the hidden units to the output are learned from the set of examples, that is input-output pairs. In principle two networks sharing the same hidden units but with different weights (from the hidden units to the output unit), could be trained to perform different tasks such as pose estimation or view-invariant recognition. Depending just on the set of training examples, learning networks of this type can learn to categorize across exemplars of a class (Riesenhuber AI Memo, 2000) as well as to identify an object across different illuminations and different viewpoints. The demonstration (Poggio, 1990) that a view-based GRBF model could achieve view-invariant object recognition in fact motivated psychophysical experiments (Buelthoff, 1992; Gauthier, 1997). In turn the psychophysics provided strong support for the view-based hypothesis against alternative theories (for a review see Tarr (1998)) and, together with the model, triggered the physiological work of Logothetis (1995).
Thus, the two key ideas in the model are:
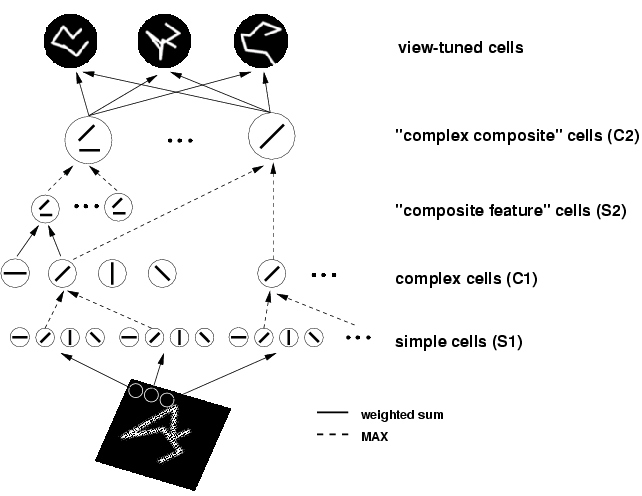
Figure 2: The basic HMAX model consists of a hierarchy of five levels, from the S1 layer with simple-cell like response properties to the VTU level with shape tuning and invariance properties like the view-tuned cells found in monkey inferotemporal cortex (see Logothetis et al., 1995).
For more information, please see the original publications. The basic model is described in the 1999 Nature Neuroscience paper:
Riesenhuber, M. & Poggio, T. (1999). Hierarchical Models of Object Recognition in Cortex. Nature Neuroscience 2: 1019-1025.
More details on how tuning properties, in particular invariance ranges in HMAX depend on pooling parameters, can be found in:
Serre, T., & Riesenhuber, M. (2004). Realistic Modeling of Simple and Complex Cell Tuning in the HMAX Model, and Implications for Invariant Object Recognition in Cortex. CBCL Paper #239/AI Memo #2004‒004, Massachusetts Institute of Technology, Cambridge, MA, July 2004.
More recent version of HMAX incorporates feature-learning at the intermediate and higher stages of the hierarchy. For a description of the four levels of the model (S1, C1, S2, C2), feature-learning operations, and performance of the model on various tasks please see the following publication:
Serre, T., Wolf, L., Bileschi, S., Riesenhuber, M., & Poggio, T. (2007). Robust Object Recognition with Cortex-like Mechanisms. IEEE Transactions on Pattern Analysis and Machine Intelligence 29(3): 411-426.
The programs provided on this website are provided 'as is' without warranty of any kind. We make no warranties, express or implied, that the programs are free of error, or are consistent with any particular standard of merchantability, or that they will meet your requirements for any particular application. They should not be relied upon for solving a problem whose incorrect solution could result in injury to a person or loss of property. If you do use the programs or procedures in such a manner, it is at your own risk. The authors disclaim all liability for direct, incidental or consequential damages resulting from your use of the programs on this website.
The full package of the code can be found in this HMAX tarball. This package implements the basic architecture of the model (S1, C1, S2, C2) and comes with a dictionary of universal features learned from a set of random natural images. Please start by reading the README file. Please note that due to the volume of inquiries, we cannot respond to individual emails about the code.